FIXED BEAM DEFLECTION CALCULATOR

Fixed beam deflection calculator for bending moment, deflection and slope calculation of a fixed beam under point load, distributed load and bending moment.

INPUT PARAMETERS
POINT LOADS
Fixed Beam Point Loading
Param. Magnitude Distance
Load 1 [P1] *
Load 2 [P2] *
Load 3 [P3] *
Load 4 [P4] *
Load 5 [P5] *
CONCENTRATED MOMENTS
Fixed Beam Concentrated Moment
Param. Magnitude Distance
Moment 1 [M1] *
Moment 2 [M2] *
Moment 3 [M3] *
Moment 4 [M4] *
Moment 5 [M5] *
DISTRIBUTED LOADS
Fixed Beam Distributed Load
Param. Magnitude Distance
wa wb a b
Distributed Load 1 [w1] *
Distributed Load 2 [w2] *
Distributed Load 3 [w3] *
Distributed Load 4 [w4] *
Distributed Load 5 [w5] *
STRUCTURAL BEAM PROPERTIES
Param. Value
Beam Length [L]
Distance x
Modulus of Elasticity [E]
Distance from neutral axis to extreme fibers [c]
Second moment of area [I] **

Note : Use dot "." as decimal separator.

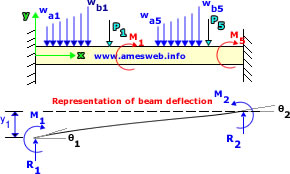
Note * : P is positive in downward direction as shown in the figure and negative in upward direction. M is positive in clockwise direction as shown in the figure. wa and wb are positive in downward direction as shown in the figure and negative in upward direction.

Note ** : For second moment of area calculations of structural beams, visit " Sectional Properties Calculators".


INPUT LOADING TO FIXED BEAM
POINT LOADS
CONCENTRATED MOMENTS
DISTRIBUTED LOADS
RESULTS
Fixed Beam Deflected
Parameter Value
Reaction Force 1 [R1]  ---
Reaction Force 2 [R2] ---
Transverse Shear Force @ distance x [Vx] ---
Maximum Transverse Shear Force [Vmax] ---
Reaction Moment 1 [M1] ---
Reaction Moment 2 [M2] ---
Moment @ distance x [Mx] ---
Maximum Moment [Mmax] ---
Slope 1 [θ1] ---
Slope 2 [θ2] ---
Slope @ distance x [θx] ---
Maximum Slope [θmax] ---
End Deflection 1 [y1] ---
End Deflection 2 [y2] ---
Deflection @ distance x [yx] ---
Maximum Deflection [ymax] ---
Bending Stress @ distance x [σx] ---
Maximum Bending Stress [σmax] ---

Note * : R1 and R2 are vertical end reactions at the left and right, respectively, and are positive upward. Shear forces and deflections are positive in upward direction and negative in downward direction. M1 and M2 are the reaction end moments at the left and right, respectively. All moments are positive when producing compression on the upper portion of the beam cross section. All slopes are positive when up and to the right.

Note: Stresses are positive numbers, and these are stress magnitudes in the beam. It does not distinguish between tension or compression of the structural beam. This distinction depends on which side of the beam's neutral plane c input corresponds.



Slope


Deflection



Moment




Shear Force

Definitions:

Distributed load: A load which acts evenly over a structural member or over a surface that supports the load.

Fixed support: Fixed supports can resist vertical and horizontal forces as well as a moment. Since they restrain both rotation and translation, they are also known as rigid supports.

Pin support: A pinned support resist both vertical and horizontal forces but not a moment. They will allow the structural member to rotate, but not to translate in any direction. A pinned connection could allow rotation in only one direction; providing resistance to rotation in any other direction.

Roller support: Roller supports are free to rotate and translate along the surface upon which the roller rests. The resulting reaction force is always a single force that is perpendicular to the surface. Roller supports are commonly located at one end of long bridges to allow the expansion and contraction of the structure due to temperature changes.

Fixed beam: A beam which is fixed at both ends.

Structural beam: A structural element that withstands loads and moments. General shapes are rectangular sections, I beams, wide flange beams and C channels.

Supplements:

Reference: