SHOULDER FILLET IN A STEPPED CIRCULAR SHAFT

Shoulder fillet in a stepped circular shaft. Stress concentration factors (Kt) for tension, bending and torsion loads.

Stress concentration factors for shoulder fillet in stepped circular shaft
 INPUT PARAMETERS
Parameter Value
Diameter of larger shaft section [D]
Diameter of smaller shaft section [d]
Radius [r]
Tension force [P]
Bending moment [M]
Torque [T]


Note: Use dot "." as decimal separator.

 


 RESULTS
LOADING TYPE - TENSION
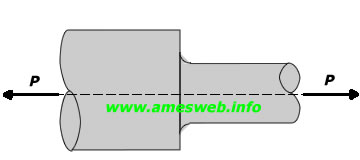
Stress concentration factors for shoulder fillet in stepped circular shaft under tension
Parameter Value
Stress concentration factor [Kt] * --- ---
Nominal tension stress at shaft [σnom ] o ---
Maximum tension stress due to tension load [σmax ] ---
LOADING TYPE - BENDING
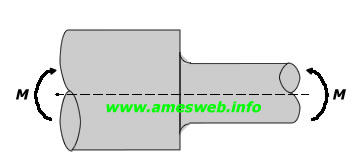
Stress concentration factors for shoulder fillet in stepped circular shaft under bending
Parameter Value
Stress concentration factor [Kt] * --- ---
Nominal tension stress at shaft [σnom ] + ---
Maximum tension stress due to bending [σmax ] ---
LOADING TYPE - TORSION
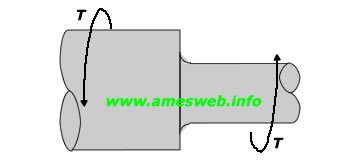
Stress concentration factors for shoulder fillet in stepped circular shaft under torsion
Parameter Value
Stress concentration factor [Kt] ** --- ---
Nominal shear stress at shaft [τnom ] x ---
Maximum shear stress due to torsion [τmax ] ---

Note 1: * Geometry rises σnom by a factor of Kt . (Kt = σmax/σnom)

Note 2: ** Geometry rises τnom by a factor of Kt . (Kt = τmax/τnom)

Note 3: o σnom = 4P/(πd2) (Nominal tension stress occurred due to tension load)

Note 4: + σnom = 32M/(πd3) (Nominal tension stress occurred due to bending)

Note 5: x τnom = 16T/(πd3) (Nominal shear stress occurred due to torsion)


Definitions:

Stress Concentration Factor: Dimensional changes and discontinuities of a member in a loaded structure causes variations of stress and high stresses concentrate near these dimensional changes. This situation of high stresses near dimensional changes and discontinuities of a member (holes, sharp corners, cracks etc.) is called stress concentration. The ratio of peak stress near stress riser to average stress over the member is called stress concentration factor.

Kt: Theoretical stress concentration factor in elastic range = (σmax/σnom)

Formulas:

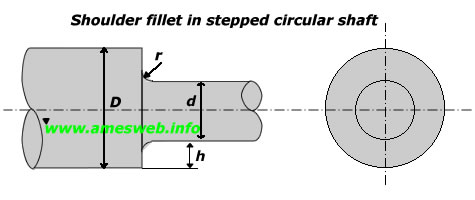
Stress concentration factors for shoulder fillet in stepped circular shaft
Tension
Stress concentration factors for shoulder fillet in stepped circular shaft under tension
$$0.1\le h/r\le 2.0$$ $$2.0\le h/r\le 20.0$$
$${ C }_{ 1 }=0.926+1.157\sqrt { h/r } -0.099h/r$$ $${ C }_{ 1 }=1.200+0.860\sqrt { h/r } -0.022h/r$$
$${ C }_{ 2 }=0.012-3.036\sqrt { h/r } +0.961h/r$$ $${ C }_{ 2 }=-1.805-0.346\sqrt { h/r } -0.038h/r$$
$${ C }_{ 3 }=-0.302+3.977\sqrt { h/r } -1.744h/r$$ $${ C }_{ 3 }=2.198-0.486\sqrt { h/r } +0.165h/r$$
$${ C }_{ 4 }=0.365-2.098\sqrt { h/r } +0.878h/r$$ $${ C }_{ 4 }=-0.593-0.028\sqrt { h/r } -0.106h/r$$
$${ K }_{ t }={ C }_{ 1 }+{ C }_{ 2 }(2h/D)+{ { C }_{ 3 }(2h/D) }^{ 2 }+{ { C }_{ 4 }(2h/D) }^{ 3 }$$
$${ \sigma }_{ nom }={ 4P }/{ \pi { d }^{ 2 } }$$
$${ \sigma }_{ max }={ K }_{ t }{ \sigma }_{ nom }$$
Bending
Stress concentration factors for shoulder fillet in stepped circular shaft under bending
$$0.1\le h/r\le 2.0$$ $$2.0\le h/r\le 20.0$$
$${ C }_{ 1 }=0.947+1.206\sqrt { h/r } -0.131h/r$$ $${ C }_{ 1 }=1.232+0.832\sqrt { h/r } -0.008h/r$$
$${ C }_{ 2 }=0.022-3.405\sqrt { h/r } +0.915h/r$$ $${ C }_{ 2 }=-3.813+0.968\sqrt { h/r } -0.260h/r$$
$${ C }_{ 3 }=0.869+1.777\sqrt { h/r } -0.555h/r$$ $${ C }_{ 3 }=7.423-4.868\sqrt { h/r } +0.869h/r$$
$${ C }_{ 4 }=-0.810+0.422\sqrt { h/r } -0.260h/r$$ $${ C }_{ 4 }=-3.839+3.070\sqrt { h/r } -0.600h/r$$
$${ K }_{ t }={ C }_{ 1 }+{ C }_{ 2 }(2h/D)+{ { C }_{ 3 }(2h/D) }^{ 2 }+{ { C }_{ 4 }(2h/D) }^{ 3 }$$
$${ \sigma }_{ nom }={ 32M }/{ \pi { d }^{ 3 } }$$
$${ \sigma }_{ max }={ K }_{ t }{ \sigma }_{ nom }$$
Torsion
Stress concentration factors for shoulder fillet in stepped circular shaft under torsion
$$0.25\le h/r\le 4.0$$
$${ C }_{ 1 }=0.905+0.783\sqrt { h/r } -0.075h/r$$
$${ C }_{ 2 }=-0.437-1.969\sqrt { h/r } +0.553h/r$$
$${ C }_{ 3 }=1.557+1.073\sqrt { h/r } -0.578h/r$$
$${ C }_{ 4 }=-1.061+0.171\sqrt { h/r } +0.086h/r$$
$${ K }_{ t }={ C }_{ 1 }+{ C }_{ 2 }(2h/D)+{ { C }_{ 3 }(2h/D) }^{ 2 }+{ { C }_{ 4 }(2h/D) }^{ 3 }$$
$${ \tau }_{ nom }={ 16T }/{ \pi { d }^{ 3 } }$$
$${ \tau }_{ max }={ K }_{ t }{ \tau }_{ nom }$$

Examples:

Reference: