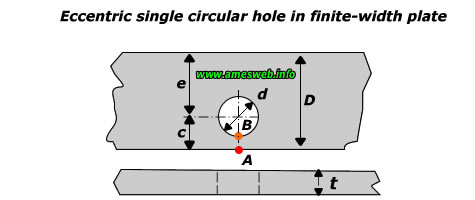
ECCENTRIC SINGLE CIRCULAR HOLE IN FINITE-WIDTH PLATE


Eccentric single circular hole in a plate. Stress concentration factors calculator (Kt) for tension and bending loads.

Stress concentration factors for central single circular hole in finite-width plate
 INPUT PARAMETERS
Parameter Value
Plate width [D]
Hole diameter [d]
Plate thickness [t]
Edge distance [c]
Distributed tension force [P]
Bending moment [M]

Note: Use dot "." as decimal separator.

 


 RESULTS
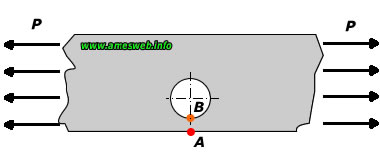
LOADING TYPE - TENSION
Stress concentration factors for central single circular hole in finite-width plate under tension
Parameter Value
Stress concentration factor [Kt] * --- ---
Nominal tension stress [σnom] o ---
Maximum tension stress (at Point-B) [σmax] ---
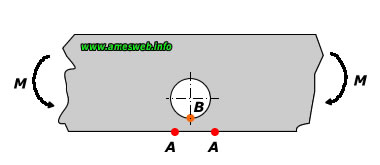
LOADING TYPE - BENDING
Stress concentration factors for central single circular hole in finite-width plate under bending
Parameter Value
At Edge of Plate
Stress concentration factor at point - A  [KtA] * --- ---
Nominal tension stress [σnom ] + ---
Maximum tension stress (at Point-A) [σmax ] ---
At Edge of Hole
Stress concentration factor at point - B [KtB] * --- ---
Nominal tension stress [σnom] x ---
Maximum tension stress (at Point-B) [σmax ] ---

Note 1: * Geometry rises σnom by a factor of Kt . (Kt = σmax/σnom)

Note 2: o For the formula, check List of Equation section.

Note 3: + σnom  = 6M/[tD2] (Nominal tension stress at the edge of plate due to bending)

Note 4: x σnom = 6M/[tD2] (Nominal tension stress at the edge of hole due to bending)

Note 5: KtA  = (σmax/σnom) Theoretical stress concentration factor at point A in elastic range

Note 6: KtB  = (σmax/σnom) Theoretical stress concentration factor at point B in elastic range

Definitions:

Stress Concentration Factor: Dimensional changes and discontinuities of a member in a loaded structure causes variations of stress and high stresses concentrate near these dimensional changes. This situation of high stresses near dimensional changes and discontinuities of a member (holes, sharp corners, cracks etc.) is called stress concentration. The ratio of peak stress near stress riser to average stress over the member is called stress concentration factor.

Kt: Theoretical stress concentration factor in elastic range = (σmax/σnom)

Supplements:

Formulas:


Stress concentration factors for central single circular hole in finite-width plate
Tension
Stress concentration factors for central single circular hole in finite-width plate under tension
$${ K }_{ t }=3.000-3.140\frac { d }{ 2c } +3.667{ \left( \frac { d }{ 2c } \right) }^{ 2 }-1.527{ \left( \frac { d }{ 2c } \right) }^{ 3 }$$
$${ \sigma }_{ nom }=\frac { P\sqrt { 1-{ \left( d/2c \right) }^{ 2 } } }{ Dt(1-d/2c) } \frac { 1-c/D }{ 1-(c/D)\left[ 2-\sqrt { 1-{ (d/2c) }^{ 2 } } \right] } $$
$${ \sigma }_{ max }={ \sigma }_{ B }={ K }_{ t }{ \sigma }_{ nom }$$
Bending
Stress concentration factors for central single circular hole in finite-width plate under bending
For Point B $$0\le d/2c\le 0.5,\quad 0\le c/e\le 1.0$$
$${ C }_{ 1 }=3.000-0.631(d/2c)+4.007{ \left( d/2c \right) }^{ 2 }$$
$${ C }_{ 2 }=-5.083+4.067(d/2c)-2.795{ \left( d/2c \right) }^{ 2 }$$
$${ C }_{ 3 }=2.114-1.682(d/2c)-0.273{ \left( d/2c \right) }^{ 2 }$$
$${ K }_{ tB }={ C }_{ 1 }+{ C }_{ 2 }\frac { c }{ e } +{ C }_{ 3 }{ (\frac { c }{ e } ) }^{ 2 }$$
$${ \sigma }_{ nom }={ 6M }/{ t{ D }^{ 2 } }$$
$${ \sigma }_{ B }={ K }_{ tB }{ \sigma }_{ nom }$$
For Point A
$${ C' }_{ 1 }=1.0286-0.1638(d/2c)+2.702{ \left( d/2c \right) }^{ 2 }$$
$${ C' }_{ 2 }=-0.05863-0.1335(d/2c)-1.8747{ \left( d/2c \right) }^{ 2 }$$
$${ C' }_{ 3 }=0.18883-0.89219(d/2c)+1.5189{ \left( d/2c \right) }^{ 2 }$$
$${ K }_{ tA }={ C' }_{ 1 }+{ C' }_{ 2 }\frac { c }{ e } +{ C' }_{ 3 }{ (\frac { c }{ e } ) }^{ 2 }$$
$${ \sigma }_{ nom }={ 6M }/{ t{ D }^{ 2 } }$$
$${ \sigma }_{ A }={ K }_{ tA }{ \sigma }_{ nom }$$

Reference: