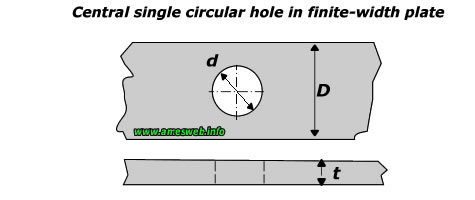
CENTRAL SINGLE CIRCULAR HOLE IN FINITE-WIDTH PLATE

Central single circular hole in finite width plate. Stress concentration factors (K_t) for tension, in-plane and simple transverse bending loads.

INPUT PARAMETERS
Parameter	Value
Plate width [D]		mm cm m inch ft
Hole diameter [d]
Plate thickness [t]
Tension force [P]		N kN lbf
In-plane bending moment [M]		N*m lbf*in lbf*ft
Transverse bending moment [M1]

Note: Use dot "." as decimal separator.

Please Wait... 

RESULTS
LOADING TYPE - TENSION
Parameter	Value
Stress concentration factor [Kt] *	---	---
Nominal tension stress [σnom ] o	---	MPa psi ksi
Maximum tension stress at the edge of hole [σmax ]	---
LOADING TYPE - IN-PLANE BENDING
Parameter	Value
At Edge of Hole
Stress concentration factor at point - A [KtA] *	---	---
Nominal tension stress [σnom ] +	---	MPa psi ksi
Maximum tension stress (at Point-A) [σmax ]	---
At Edge of Plate
Stress concentration factor at point - B [KtB] *	---	---
Nominal tension stress [σnom] x	---	MPa psi ksi
Maximum tension stress (at Point-B) [σmax ]	---
LOADING TYPE - SIMPLE TRANSVERSE BENDING
Stress concentration factor at point A[KtA] *	---	---
Nominal tension stress [σnom ] #	---	MPa psi ksi
Maximum tension stress (at Point-A) [σmax ]	---

Note 1: * Geometry rises σ_nom by a factor of K_t . (K_t = σ_max/σ_nom)

Note 2: ^o σ_nom= P/[t(D-d)] (Nominal tension stress at the plate cross section due to tension load)

Note 3: ⁺ σ_nom  = 6Md/[t(D³-d³)] (Nominal tension stress at the edge of hole due to bending)

Note 4: ^x σ_nom = 6MD/[t(D³-d³)] (Nominal tension stress at the edge of plate due to bending)

Note 5: ^# σ_nom = 6M₁/[t²(D-d)] (Nominal tension stress at the edge of plate due to bending)

Note 6: α=30°

Note 7: K_tA  = (σ_max/σ_nom) Theoretical stress concentration factor at point A in elastic range

Note 8: K_tB  = (σ_max/σ_nom) Theoretical stress concentration factor at point B in elastic range

Definitions:

Stress Concentration Factor: Dimensional changes and discontinuities of a member in a loaded structure causes variations of stress and high stresses concentrate near these dimensional changes. This situation of high stresses near dimensional changes and discontinuities of a member (holes, sharp corners, cracks etc.) is called stress concentration. The ratio of peak stress near stress riser to average stress over the member is called stress concentration factor.

K_t: Theoretical stress concentration factor in elastic range = (σ_max/σ_nom)

Supplements:

• Eccentric Single Circular Hole in Finite Width Plate

Formulas:

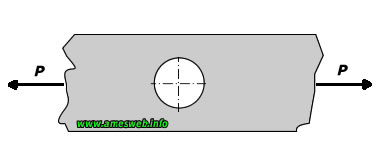
Tension

For $$0\le \frac { d }{ D } \le 1$$

$$3.000-3.140\frac { d }{ D } +3.667{ \left( \frac { d }{ D } \right) }^{ 2 }-1.527{ \left( \frac { d }{ D } \right) }^{ 3 }$$

$${ \sigma }_{ nom }=P/[(D-d)t]$$

$${ \sigma }_{ max }={ K }_{ t }{ \sigma }_{ nom }$$

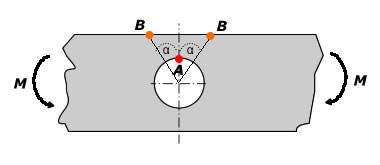
In-Plane Bending

At the edge of hole

Kta = 2 (independent of d/D)

$${ \sigma }_{ nom }=6Md/[({ D }^{ 3 }-{ d }^{ 3 })t]$$

σmax@A = Ktσnom

At the edge of plate

$${ K }_{ tb }=\frac { 2d }{ D } (\alpha ={ 30 }^{ \circ })$$

$${ \sigma }_{ nom }=6MD/[({ D }^{ 3 }-{ d }^{ 3 })t]$$

σmax@B = Ktσnom

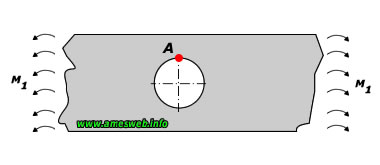
Simple Transverse  Bending

For $$0\le \cfrac { d }{ D } \le 0.3$$ and $$1\le d/t\le 7$$

$${ K }_{ t }=\left[ 1.793+\frac { 0.131 }{ d/t } +\frac { 2.052 }{ { \left( d/t \right) }^{ 2 } } -\frac { 1.019 }{ { \left( d/t \right) }^{ 3 } } \right] \times \left[ 1-1.04(d/D)+1.22{ (d/D) }^{ 2 } \right]$$

$${ \sigma }_{ nom }=6{ M }_{ 1 }/[(D-d){ t }^{ 2 }]$$

σmax@A = Ktσnom

Reference:

• Pilkey, W. D..(2005). Formulas for Stress, Strain, and Structural Matrices Formulas for Stress, Strain, and Structural Matrices .2nd Edition John Wiley & Sons