Fixed fixed beam natural frequency calculator to calculate natural frequency of
a uniform beam with both ends fixed. The natural frequency formulas used for calculations are given below the calculator.
Note: Use dot "." as decimal separator.
|
RESULTS |
|
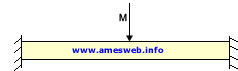
Center load M, beam weight negligible |
|
|
Parameter |
Value |
|
First natural frequency [f1] |
---
|
Hz |
|
Uniform load w per unit length including beam weight |

|
|
Parameter |
Value |
|
First natural frequency [f1] |
---
|
Hz |
|
Second natural frequency [f2] |
---
|
|
Third natural frequency [f3] |
---
|
|
Forth natural frequency [f4] |
---
|
|
Fifth natural frequency [f5] |
---
|
|
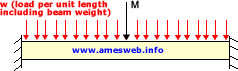
Uniform load w per unit length plus a center load M (approximately) |
|
|
Parameter |
Value |
|
First natural frequency [f1] |
---
|
Hz |