DOT PRODUCT CALCULATOR

Dot product calculator calculates dot product (scalar product), magnitudes and angle between two vectors. The calculator can be used for dot product calculation of 2D or 3D vectors.

Dot product calculation can be done for two different vector forms: vector components or magnitudes and angle between vectors.

What is the formula for dot product of vectors?

The dot product formulas used for the calculations are given below.

Dot product of vectors $$\vec { A } \cdot \vec { B }={ A}_{ x }{ B }_{ x}+{ A}_{ y }{ B }_{y}+{ A}_{ z }{ B }_{z}$$
Dot product by magnitudes and cosine angle $$\vec { A } \cdot \vec { B } =\left| A \right| \left| B \right| \cos { \theta }$$

Dot Product Calculator:

Dot Product Vector Magnitudes
INPUT PARAMETERS
Vector Form:
VECTOR COMPONENTS
Vector
MAGNITUDES AND ANGLE
|A| |B| θ (deg)





Note: Use dot "." as decimal separator.



RESULTS
Parameter Symbol Value Unit
Dot Product of Vectors A and B --- ---
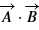
Magnitude of Vector A |A| ---
Magnitude of Vector B |B| ---
Angle between Vectors θ --- deg

What is dot product?

Dot Product is a type of vector multiplication and the result is scalar and it has no longer a direction.

What are the properties of dot product?

  • The dot product is commutative.

 $$\overrightarrow{a} \cdot \overrightarrow{b} = \overrightarrow{b} \cdot \overrightarrow{a}$$

  • The dot product is distributive.

$$\overrightarrow{a} \cdot (\overrightarrow{b} + \overrightarrow{c}) = \overrightarrow{a} \cdot \overrightarrow{b} + \overrightarrow{a} \cdot \overrightarrow{c}$$  

  • The dot product is associative concerning scalar multiplication. A scalar times vector involved in a dot product is the same as the scalar multiplied by the dot product.

$$(\lambda \overrightarrow{a}) \cdot \overrightarrow{b} =\lambda \cdot (\overrightarrow{a} + \overrightarrow{b})= \overrightarrow{a} \cdot (\lambda \overrightarrow{b})$$

  • The dot product of vector itself is simply the square of the magnitude of the vector.
    • $$\overrightarrow{a} \cdot \overrightarrow{a} = \left| a \right|^{2}$$

Supplements:

Reference: