V-SHAPED CIRCUMFERENTIAL GROOVE

V-shaped circumferential groove on a shaft. Stress concentration factors (K_t) calculator for torsion loads.

INPUT PARAMETERS
Parameter	Value
Diameter of larger shaft section [D]		mm cm m inch ft
Diameter of smaller shaft section [d]
Radius [r]
Angle [θ]		deg
Torque [T]		N*m lbf*in lbf*ft

Note: Use dot "." as decimal separator.

Please Wait... 

RESULTS
LOADING TYPE - TORSION
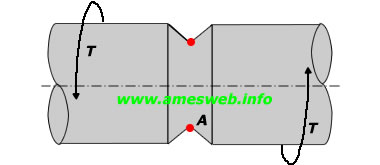
Parameter	Value
Stress concentration factorn [Kt] *	---	---
Nominal shear stress at shaft [τnom ] x	---	MPa psi ksi
Maximum shear stress due to torsion (at Point-A) [τmax ]	---

Note 1: Maximum stress is occured at point A.

Note 2: * Geometry rises τ_nom by a factor of K_t. (K_t = τ_nom/τ_max)

Note 3: ^x τ_nom= 16T/(πd³) (Nominal shear stress occurred due to torsion)

Note 4: V-shaped stress concentration factor is dependent on U-shaped stress concentration factor. Input parameters shall satisfy both cases.

Definitions:

Stress Concentration Factor: Dimensional changes and discontinuities of a member in a loaded structure causes variations of stress and high stresses concentrate near these dimensional changes. This situation of high stresses near dimensional changes and discontinuities of a member (holes, sharp corners, cracks etc.) is called stress concentration. The ratio of peak stress near stress riser to average stress over the member is called stress concentration factor.

K_t: Theoretical stress concentration factor in elastic range = (σ_max/σ_nom)

Formulas:

Torsion

0°≤ θ ≤90°, Kt is independent of r/d  90°≤ θ ≤ 125°, Kt is applicable only if r/d ≤ 0.01.

$${ C }_{ 1 }=0.2026\sqrt { \theta } -0.06620\theta +0.00281\theta \sqrt { \theta }$$

$${ C }_{ 2 }=-0.2226\sqrt { \theta } +0.07814\theta -0.002477\theta \sqrt { \theta }$$

$${ C }_{ 3 }=1+0.0298\sqrt { \theta } -0.01485\theta -0.000151\theta \sqrt { \theta }$$

Ktu=Stress concentration factor for U-shaped groove (θ=0)

$${ C }_{ t }={ C }_{ 1 }+{ C }_{ 2 }\sqrt { { K }_{ tu } } +{ C }_{ 3 }{ K }_{ tu }$$

τnom=16T/πd3

τmax=τA=Ktτnom

Reference:

• Pilkey, W. D..(2005). Formulas for Stress, Strain, and Structural Matrices Formulas for Stress, Strain, and Structural Matrices .2nd Edition John Wiley & Sons