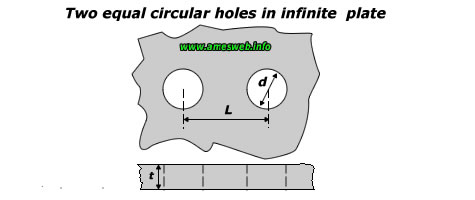
TWO EQUAL CIRCULAR HOLES IN AN INFINITE PLATE

Two equal circular holes in an infinite plate. Stress concentration factors (K_t) calculator for tension loads.

INPUT PARAMETERS
Parameter	Value
Hole diameter [d]		mm cm m inch ft
Distance between hole centers [L]
Plate thickness [t]
In-plane normal stress [σ]		MPa psi ksi

Note: Use dot "." as decimal separator.

Please Wait... 

RESULTS
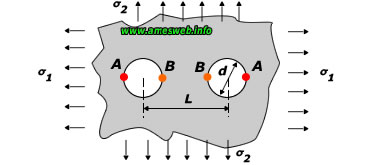
LOADING TYPE - IN-PLANE NORMAL STRESSES
Parameter	Value
UNIAXIAL TENSION PARALLEL TO ROW OF HOLES (σ1=σ ,σ2=0)
Stress concentration factor [Kt] *	---	---
Maximum tension stress [σ]	---	MPa psi ksi
UNIAXIAL TENSION NORMAL TO ROW OF HOLES (σ1=0 ,σ2=σ)
Stress concentration factor for point-B [KtB]*	---	---
Nominal tension stress [σnom]	---	MPa psi ksi
Maximum tension stress at point-B [σB]	---
BIAXIAL STRESS ( σ2 = σ1)
Stress concentration factor for point-B [KtB]*	---	---
Nominal tension stress [σnom]	---	MPa psi ksi
Maximum tension stress at point-B [σB]	---

Note 1: * Geometry rises σ_nom by a factor of K_t . (K_t = σ_max/σ_nom)

Note 2: K_tB  = (σ_max/σ_nom) Theoretical stress concentration factor at point B in elastic range

Definitions:

Stress Concentration Factor: Dimensional changes and discontinuities of a member in a loaded structure causes variations of stress and high stresses concentrate near these dimensional changes. This situation of high stresses near dimensional changes and discontinuities of a member (holes, sharp corners, cracks etc.) is called stress concentration. The ratio of peak stress near stress riser to average stress over the member is called stress concentration factor.

K_t: Theoretical stress concentration factor in elastic range = (σ_max/σ_nom)

Formulas:

Tension

for 0 ≤ d/L<1

$${ \sigma }_{ max }={ K }_{ t }\sigma$$

Uniaxial tension parallel to row of holes (σ1 = σ , σ2 = 0) $${ K }_{ t }=3.000-0.712d/L+0.271{ (d/L) }^{ 2 }$$

Uniaxial tension normal to row of holes (σ2 = σ , σ1 = 0) $${ \sigma }_{ max }={ \sigma }_{ B }={ K }_{ t }{ \sigma }_{ nom }\quad ,\quad { \sigma }_{ nom }\quad =\frac { \sigma \sqrt { 1-{ \left( d/L \right) }^{ 2 } } }{ 1-d/L }$$ $${ K }_{ t }=3.000-3.0018d/L+1.0099{ (d/L) }^{ 2 }$$

Biaxial tension (σ2 = σ, σ1 = σ) $${ \sigma }_{ max }={ \sigma }_{ B }={ K }_{ t }{ \sigma }_{ nom }\quad ,\quad { \sigma }_{ nom }\quad =\frac { \sigma \sqrt { 1-{ \left( d/L \right) }^{ 2 } } }{ 1-d/L }$$ $${ K }_{ t }=2.000-2.119d/L+2.493{ (d/L) }^{ 2 }-1.372{ (d/L) }^{ 3 }$$

Reference:

• Pilkey, W. D..(2005). Formulas for Stress, Strain, and Structural Matrices Formulas for Stress, Strain, and Structural Matrices .2nd Edition John Wiley & Sons