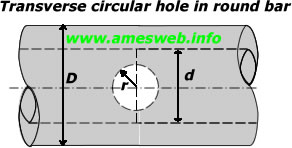
TRANSVERSE CIRCULAR HOLE IN A ROUND BAR

Transverse circular hole in round bar. Stress concentration factors (Kt) for tension, bending and torsion loads.

Stress concentration factors of transverse circular hole in round bar
 INPUT PARAMETERS
Parameter Value
Diameter of shaft [D]
Hollow shaft inner diameter [d]
Transverse hole radius [r]
Tension force [P]
Bending moment [M]
Torque [T]


Note: Use dot "." as decimal separator.


 RESULTS
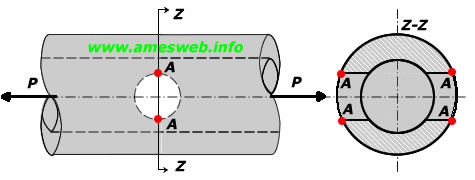
LOADING TYPE - TENSION
Stress concentration factors of transverse circular hole in round bar in tension
Parameter Value
Stress concentration factor [Kt] * --- ---
Nominal tension stress at shaft [σnom ] o ---
Maximum tension stress due to tension load (at Point-A) [σmax ] ---
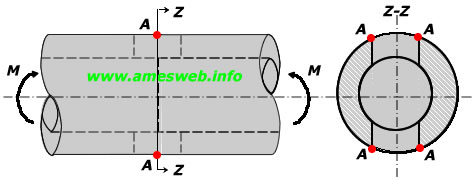
LOADING TYPE - BENDING
Stress concentration factors of transverse circular hole in round bar in bending
Parameter Value
Stress concentration factor [Kt] * --- ---
Nominal tension stress at shaft [σnom ] + ---
Maximum tension stress due to bending (at Point-A) [σmax ] ---
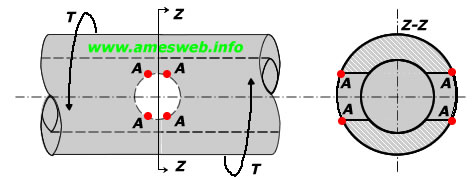
LOADING TYPE - TORSION
Stress concentration factors of transverse circular hole in round bar in torsion
Parameter Value
Stress concentration factor [Kt] ** --- ---
Nominal shear stress at shaft [τnom ] x ---
Maximum shear stress due to torsion (at Point-A) [τmax ] ---
Maximum tension stress due to torsion (at Point-A) [σmax] ---

Note 1: Maximum stress is occured at point A.

Note 2: * Geometry rises σnom by a factor of Kt . (Kt = σmax/σnom)

Note 3: ** Geometry rises τnom by a factor of Kt . (Kt = 2*τmax/τnom)

Note 4: o σnom = 4P/[π(D2 - d2)] (Nominal tension stress occurred due to tension load)

Note 5: + σnom= (32MD)/[π(D4-d4)] (Nominal tension stress occurred due to bending)

Note 6: x τnom = (16TD)/[π(D4-d4)] (Nominal shear stress occurred due to torsion)


Definitions:

Stress Concentration Factor: Dimensional changes and discontinuities of a member in a loaded structure causes variations of stress and high stresses concentrate near these dimensional changes. This situation of high stresses near dimensional changes and discontinuities of a member (holes, sharp corners, cracks etc.) is called stress concentration. The ratio of peak stress near stress riser to average stress over the member is called stress concentration factor.

Kt: Theoretical stress concentration factor in elastic range = (σmax/σnom)

Formulas:

Stress concentration factors of transverse circular hole in round bar
Tension
Stress concentration factors of transverse circular hole in round bar in tension
$$d/D\le 0.9\quad ,\quad 2r/D\le 0.45$$
$${ C }_{ 1 }=3.0$$
$${ C }_{ 2 }=0.427-6.770\frac { d }{ D } +22.698{ (\frac { d }{ D } ) }^{ 2 }-16.670{ (\frac { d }{ D } ) }^{ 3 }$$
$${ C }_{ 3 }=11.357+15.665\frac { d }{ D } -60.929{ (\frac { d }{ D } ) }^{ 2 }+41.501{ (\frac { d }{ D } ) }^{ 3 }$$
$${ K }_{ t }={ C }_{ 1 }+{ C }_{ 2 }\frac { 2r }{ D } +{ C }_{ 3 }{ \left( \frac { 2r }{ D } \right) }^{ 2 }$$
$${ \sigma }_{ nom }=\frac { 4P }{ \pi ({ D }^{ 2 }-{ d }^{ 2 }) } $$
$${ \sigma }_{ max }={ \sigma }_{ A }={ K }_{ t }{ \sigma }_{ nom }$$
Bending
Stress concentration factors of transverse circular hole in round bar in bending
$$d/D\le 0.9\quad ,\quad 2r/D\le 0.4$$
$${ C }_{ 1 }=3.0$$
$${ C }_{ 2 }=-6.250-0.585\frac { d }{ D } +3.115{ (\frac { d }{ D } ) }^{ 2 }$$
$${ C }_{ 3 }=41.000-1.071\frac { d }{ D } -6.746{ (\frac { d }{ D } ) }^{ 2 }$$
$${ C }_{ 4 }=-45.000+1.389\frac { d }{ D } +13.889{ (\frac { d }{ D } ) }^{ 2 }$$
$${ K }_{ t }={ C }_{ 1 }+{ C }_{ 2 }\frac { 2r }{ D } +{ C }_{ 3 }{ \left( \frac { 2r }{ D } \right) }^{ 2 }+{ C }_{ 4 }{ \left( \frac { 2r }{ D } \right) }^{ 3 }$$
$${ \sigma }_{ nom }=\frac { 32MD }{ \pi ({ D }^{ 4 }-{ d }^{ 4 }) } $$
$${ \sigma }_{ max }={ \sigma }_{ A }={ K }_{ t }{ \sigma }_{ nom }$$
Torsion
Stress concentration factors of transverse circular hole in round bar in torsion
$$d/D\le 0.8\quad ,\quad 2r/D\le 0.4$$
$${ C }_{ 1 }=4.0$$
$${ C }_{ 2 }=-6.055+3.184\frac { d }{ D } -3.461{ (\frac { d }{ D } ) }^{ 2 }$$
$${ C }_{ 3 }=32.764-30.121\frac { d }{ D } +39.887{ (\frac { d }{ D } ) }^{ 2 }$$
$${ C }_{ 4 }=-38.330+51.542\sqrt { d/D } -27.483\frac { d }{ D } $$
$${ K }_{ t }={ C }_{ 1 }+{ C }_{ 2 }\frac { 2r }{ D } +{ C }_{ 3 }{ \left( \frac { 2r }{ D } \right) }^{ 2 }+{ C }_{ 4 }{ \left( \frac { 2r }{ D } \right) }^{ 3 }$$
$${ \sigma }_{ max }={ \sigma }_{ A }={ K }_{ t }{ \tau }_{ nom }$$
$${ \tau }_{ nom }=\frac { 16TD }{ \pi ({ D }^{ 4 }-{ d }^{ 4 }) } $$
$${ \tau }_{ max }={ \tau }_{ A }={ 0.5K }_{ t }{ \tau }_{ nom }$$

Reference: