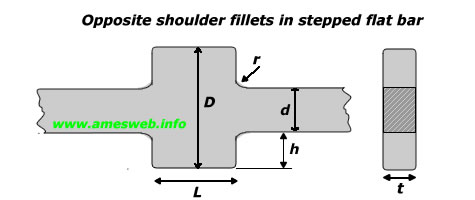
OPPOSITE SHOULDER FILLETS IN A STEPPED BAR

Opposite shoulder fillets in stepped flat bar. Stress concentration factors (Kt) calculator for tension, bending and torsion loads.

Stress concentration factors for opposite shoulder fillets in stepped bar
 INPUT PARAMETERS
Parameter Value
Thickness of stepped section  [D]
Thickness of flat section [d]
Radius [r]
Length of stepped section [L]
Width of bar[t]
Tension force [P]
Bending moment [M]

Note: Use dot "." as decimal separator.


 RESULTS
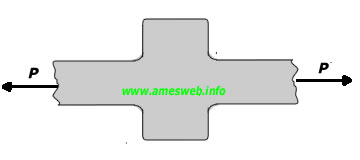
LOADING TYPE - TENSION
Stress concentration factors for opposite shoulder fillets in stepped bar under tension
Parameter Value
Stress concentration factor [Kt] * --- ---
Nominal tension stress at flat bar [σnom ] o ---
Maximum tension stress due to tension load [σmax ] ---
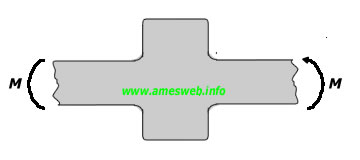
LOADING TYPE - BENDING
Stress concentration factors for opposite shoulder fillets in stepped bar under bending
Parameter Value
Stress concentration factor [Kt] * --- ---
Nominal tension stress at flat bar [σnom ] + ---
Maximum tension stress due to bending [σmax ] ---

Note 1: * Geometry rises σnom by a factor of Kt. (Kt = σmax/σnom)

Note 2: o σnom= P/(td) (Nominal tension stress occurred due to tension load)

Note 3: + σnom = 6M/(td2) (Nominal tension stress occured due to bending)


Definitions:

Stress Concentration Factor:Dimensional changes and discontinuities of a member in a loaded structure causes variations of stress and high stresses concentrate near these dimensional changes. This situation of high stresses near dimensional changes and discontinuities of a member (holes, sharp corners, cracks etc.) is called stress concentration. The ratio of peak stress near stress riser to average stress over the member is called stress concentration factor.

Kt: Theoretical stress concentration factor in elastic range = (σmax/σnom)

Formulas:

Stress concentration factors for opposite shoulder fillets in stepped bar
Tension
Stress concentration factors for opposite shoulder fillets in stepped bar under tension
$$0.1\le \frac { h }{ r } \le 2.0$$ $$2\le \frac { h }{ r } \le 20$$
$${ C }_{ 1 }=1.006+1.008\sqrt { h/r } -0.044h/r$$ $${ C }_{ 1 }=1.020+1.009\sqrt { h/r } -0.048h/r$$
$${ C }_{ 2 }=-0.115-0.584\sqrt { h/r } +0.315h/r$$ $${ C }_{ 2 }=-0.065-0.165\sqrt { h/r } -0.007h/r$$
$${ C }_{ 3 }=0.245-1.006\sqrt { h/r } -0.257h/r$$ $${ C }_{ 3 }=-3.459+1.266\sqrt { h/r } -0.016h/r$$
$${ C }_{ 4 }=-0.135+0.582\sqrt { h/r } -0.017h/r$$ $${ C }_{ 4 }=3.505-2.109\sqrt { h/r } +0.069h/r$$
$${ K }_{ t }={ C }_{ 1 }+{ C }_{ 2 }\frac { 2h }{ D } +{ C }_{ 3 }{ (\frac { 2h }{ D } ) }^{ 2 }+{ C }_{ 4 }{ (\frac { 2h }{ D } ) }^{ 3 }$$
where
$$\frac { L }{ D } >-1.89(\frac { r }{ d } -0.15)+5.5$$
$${ \sigma }_{ nom }=P/td$$
$${ \sigma }_{ max }={ K }_{ t }{ \sigma }_{ nom }$$
Bending
Stress concentration factors for opposite shoulder fillets in stepped bar under bending
$$0.1\le \frac { h }{ r } \le 2.0$$ $$2\le \frac { h }{ r } \le 20$$
$${ C }_{ 1 }=1.006+0.967\sqrt { h/r } +0.013h/r$$ $${ C }_{ 1 }=1.058+1.002\sqrt { h/r } -0.038h/r$$
$${ C }_{ 2 }=-0.270-2.372\sqrt { h/r } +0.708h/r$$ $${ C }_{ 2 }=-3.652+1.639\sqrt { h/r } -0.436h/r$$
$${ C }_{ 3 }=0.662+1.157\sqrt { h/r } -0.908h/r$$ $${ C }_{ 3 }=6.170-5.687\sqrt { h/r } +1.175h/r$$
$${ C }_{ 4 }=-0.405+0.249\sqrt { h/r } -0.200h/r$$ $${ C }_{ 4 }=-2.558+3.046\sqrt { h/r } -0.701h/r$$
$${ K }_{ t }={ C }_{ 1 }+{ C }_{ 2 }\frac { 2h }{ D } +{ C }_{ 3 }{ (\frac { 2h }{ D } ) }^{ 2 }+{ C }_{ 4 }{ (\frac { 2h }{ D } ) }^{ 3 }$$
where
$$\frac { L }{ D } >-2.05(\frac { r }{ d } -0.025)+2$$
$${ \sigma }_{ nom }={ 6M }/{ t{ d }^{ 2 } }$$
$${ \sigma }_{ max }={ K }_{ t }{ \sigma }_{ nom }$$

Reference: