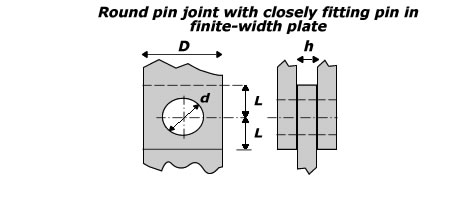
ROUND PIN JOINT WITH CLOSELY FITTING PIN IN A FINITE-WIDTH PLATE

Round pin joint with closely fitting pin in a finite width plate. Stress concentration factors (K_t) calculator for tension loads.

INPUT PARAMETERS
Parameter	Value
Plate width [D]		mm cm m inch ft
Hole diameter [d]
Hole center to plate edge distance [L]
Plate thickness [h]
Tension force [P]		N kN lbf

Note: Use dot "." as decimal separator.

Please Wait... 

RESULTS
LOADING TYPE - TENSION
Parameter	Value
TENSION STRESS
Stress concentration factor [Kta] *	---	---
Nominal tension stress based on net section [σna ] o	---	MPa psi ksi
Maximum tension stress [σmax]	---
BEARING STRESS
Stress concentration factor [Ktb] **	---	---
Nominal bearing stress based on bearing area [σnb ] x	---	MPa psi ksi
Maximum bearing stress [σmax ]	---

Note 1: * Geometry rises σ_na by a factor of K_ta. (K_ta= σ_max/σ_na)

Note 2: ** Geometry rises σ_nb by a factor of K_tb. (K_tb= σ_max/σ_nb)

Note 3: ^o Nominal stress based on net section (σ_na= P/[(D-d)h])

Note 4: ^x Nominal stress based on bearing area  (σ_nb= P/(dh))

Definitions:

Stress Concentration Factor: Dimensional changes and discontinuities of a member in a loaded structure causes variations of stress and high stresses concentrate near these dimensional changes. This situation of high stresses near dimensional changes and discontinuities of a member (holes, sharp corners, cracks etc.) is called stress concentration. The ratio of peak stress near stress riser to average stress over the member is called stress concentration factor.

K_t: Theoretical stress concentration factor in elastic range = (σ_max/σ_nom)

Formulas:

Tension

For $$0.15\le \frac { d }{ D } \le 0.75,\quad \frac { L }{ D } \ge 1$$

$${ K }_{ ta }=12.882-52.714\frac { d }{ D } +89.762{ (\frac { d }{ D } ) }^{ 2 }-51.667{ (\frac { d }{ D } ) }^{ 3 }$$

$${ K }_{ tb }=0.2880+8.820\frac { d }{ D } -23.196{ (\frac { d }{ D } ) }^{ 2 }+29.167{ (\frac { d }{ D } ) }^{ 3 }$$

Nominal stress based on net section:  $${ \sigma }_{ na }=P/(D-d)h$$

Nominal stress based on bearing area: $${ \sigma }_{ nb }=P/dh$$

$${ \sigma }_{ max\_ a }={ K }_{ t }{ \sigma }_{ na }$$

$${ \sigma }_{ max\_ b }={ K }_{ t }{ \sigma }_{ nb }$$

Reference:

• Pilkey, W. D..(2005). Formulas for Stress, Strain, and Structural Matrices Formulas for Stress, Strain, and Structural Matrices .2nd Edition John Wiley & Sons