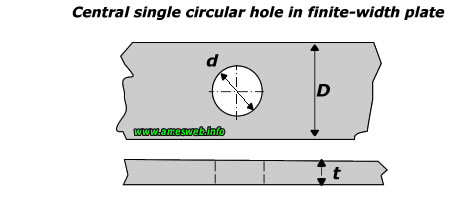
|
|
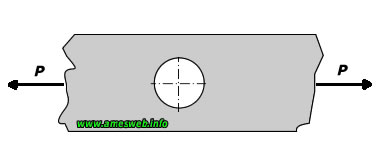
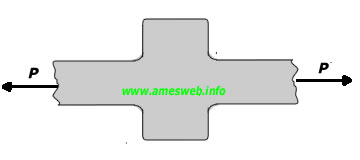
Tension |
|
|
For $$0\le \frac { d }{ D } \le 1$$ |
|
$$3.000-3.140\frac { d }{ D } +3.667{ \left( \frac { d }{ D } \right) }^{ 2
}-1.527{ \left( \frac { d }{ D } \right) }^{ 3 }$$ |
|
$${ \sigma }_{ nom }=P/[(D-d)t]$$ |
|
$${ \sigma }_{ max }={ K }_{ t }{ \sigma }_{ nom }$$ |
|
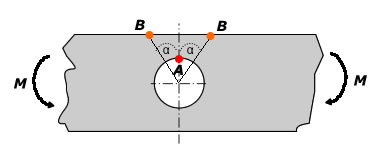
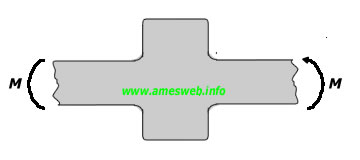
In-Plane Bending |
|
|
At the edge of hole |
|
Kta = 2 (independent of d/D) |
|
$${ \sigma }_{ nom }=6Md/[({ D }^{ 3 }-{ d }^{ 3 })t]$$ |
|
σmax@A =
Ktσnom |
|
At the edge of plate |
|
$${ K }_{ tb }=\frac { 2d }{ D } (\alpha ={ 30 }^{ \circ })$$ |
|
$${ \sigma }_{ nom }=6MD/[({ D }^{ 3 }-{ d }^{ 3 })t]$$ |
|
σmax@B = Ktσnom |
|
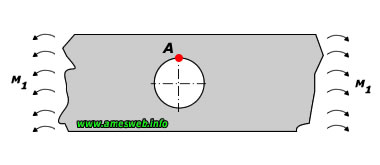
Simple Transverse Bending |
|
|
For $$0\le \cfrac { d }{ D } \le 0.3$$ and $$1\le d/t\le 7$$ |
|
$${ K }_{ t }=\left[ 1.793+\frac { 0.131 }{ d/t } +\frac { 2.052 }{ { \left( d/t
\right) }^{ 2 } } -\frac { 1.019 }{ { \left( d/t \right) }^{ 3 } } \right]
\times \left[ 1-1.04(d/D)+1.22{ (d/D) }^{ 2 } \right]$$ |
|
$${ \sigma }_{ nom }=6{ M }_{ 1 }/[(D-d){ t }^{ 2 }]$$ |
|
σmax@A = Ktσnom |
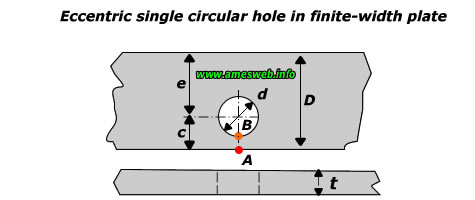
|
|
Tension |
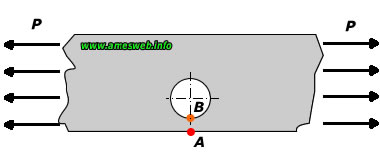
|
|
$${ K }_{ t }=3.000-3.140\frac { d }{ 2c } +3.667{ \left( \frac { d }{ 2c }
\right) }^{ 2 }-1.527{ \left( \frac { d }{ 2c } \right) }^{ 3 }$$ |
|
$${ \sigma }_{ nom }=\frac { P\sqrt { 1-{ \left( d/2c \right) }^{ 2 } } }{
Dt(1-d/2c) } \frac { 1-c/D }{ 1-(c/d)\left[ 2-\sqrt { 1-{ (d/2c) }^{ 2 } }
\right] } $$ |
|
$${ \sigma }_{ max }={ \sigma }_{ B }={ K }_{ t }{ \sigma }_{ nom }$$ |
|
Bending |
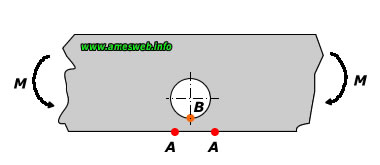
|
|
For Point B $$0\le d/2c\le 0.5,\quad 0\le c/e\le 1.0$$ |
|
$${ C }_{ 1 }=3.000-0.631(d/2c)+4.007{ \left( d/2c \right) }^{ 2 }$$ |
|
$${ C }_{ 2 }=-5.083+4.067(d/2c)-2.795{ \left( d/2c \right) }^{ 2 }$$ |
|
$${ C }_{ 3 }=2.114-1.682(d/2c)-0.273{ \left( d/2c \right) }^{ 2 }$$ |
|
$${ K }_{ tB }={ C }_{ 1 }+{ C }_{ 2 }\frac { c }{ e } +{ C }_{ 3 }{ (\frac { c
}{ e } ) }^{ 2 }$$ |
|
$${ \sigma }_{ nom }={ 6M }/{ t{ D }^{ 2 } }$$ |
|
$${ \sigma }_{ B }={ K }_{ tB }{ \sigma }_{ nom }$$ |
|
For Point A |
|
$${ C' }_{ 1 }=1.0286-0.1638(d/2c)+2.702{ \left( d/2c \right) }^{ 2 }$$ |
|
$${ C' }_{ 2 }=-0.05863-0.1335(d/2c)-1.8747{ \left( d/2c \right) }^{ 2 }$$ |
|
$${ C' }_{ 3 }=0.18883-0.89219(d/2c)+1.5189{ \left( d/2c \right) }^{ 2 }$$ |
|
$${ K }_{ tA }={ C' }_{ 1 }+{ C' }_{ 2 }\frac { c }{ e } +{ C' }_{ 3 }{ (\frac { c
}{ e } ) }^{ 2 }$$ |
|
$${ \sigma }_{ nom }={ 6M }/{ t{ D }^{ 2 } }$$ |
|
$${ \sigma }_{ A }={ K }_{ tA }{ \sigma }_{ nom }$$ |
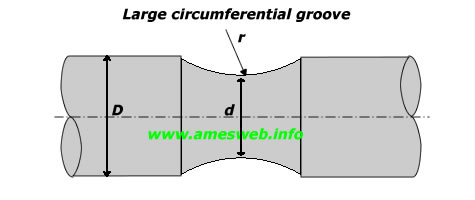
|
|
Tension |
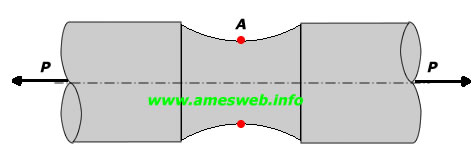
|
|
$$
0.3\quad \le \quad \frac { r }{ d } \le \quad 1.0 $$ , $$ 1.005\quad \le \quad \frac { D }{ d } \le \quad 1.10
$$ |
|
$${ C }_{ 1 }=-81.39+153.10(D/d)-70.49{ (D/d) }^{ 2 }$$ |
|
$${ C }_{ 2 }=119.64-221.81(D/d)+101.93{ (D/d) }^{ 2 }$$ |
|
$${ C }_{ 3 }=-57.88+107.33(D/d)-49.34{ (D/d) }^{ 2 }$$ |
|
$${ K }_{ t }={ C }_{ 1 }+{ C }_{ 2 }\frac { r }{ d } +{ C }_{ 3 }{ (\frac { r
}{ d } ) }^{ 2 }$$ |
|
$${ \sigma }_{ nom }=4P/\pi { d }^{ 2 }$$ |
|
$${ \sigma }_{ max }={ \sigma }_{ A }={ K }_{ t }{ \sigma }_{ nom }$$ |
|
Bending |
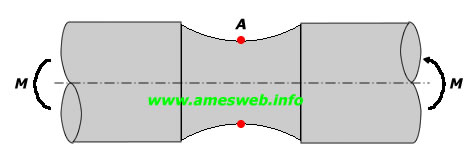
|
|
$$
0.3\quad \le \quad \frac { r }{ d } \le \quad 1.0 $$ , $$ 1.005\quad \le \quad \frac { D }{ d } \le \quad 1.10
$$ |
|
$${ C }_{ 1 }=-39.58+73.22(D/d)-32.46{ (D/d) }^{ 2 }$$ |
|
$${ C }_{ 2 }=-9.477+29.41(D/d)-20.13{ (D/d) }^{ 2 }$$ |
|
$${ C }_{ 3 }=82.46-166.96(D/d)+84.58{ (D/d) }^{ 2 }$$ |
|
$${ K }_{ t }={ C }_{ 1 }+{ C }_{ 2 }\frac { r }{ d } +{ C }_{ 3 }{ (\frac { r
}{ d } ) }^{ 2 }$$ |
|
$${ \sigma }_{ nom }=32M/\pi { d }^{ 3 }$$ |
|
$${ \sigma }_{ max }={ \sigma }_{ A }={ K }_{ t }{ \sigma }_{ nom }$$ |
|
Torsion |
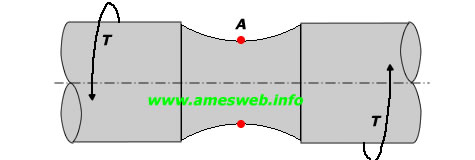
|
|
$$
0.3\quad \le \quad \frac { r }{ d } \le \quad 1.0 $$ , $$ 1.005\quad \le \quad \frac { D }{ d } \le \quad 1.10
$$ |
|
$${ C }_{ 1 }=-35.16+67.57(D/d)-31.28{ (D/d) }^{ 2 }$$ |
|
$${ C }_{ 2 }=79.13-148.37(D/d)+69.09{ (D/d) }^{ 2 }$$ |
|
$${ C }_{ 3 }=-50.34+94.67(D/d)-44.26{ (D/d) }^{ 2 }$$ |
|
$${ K }_{ t }={ C }_{ 1 }+{ C }_{ 2 }\frac { r }{ d } +{ C }_{ 3 }{ (\frac { r
}{ d } ) }^{ 2 }$$ |
|
$${ \tau }_{ nom }=16T/\pi { d }^{ 3 }$$ |
|
$${ \tau }_{ max }=\tau _{ A }={ K }_{ t }{ \tau }_{ nom }$$ |
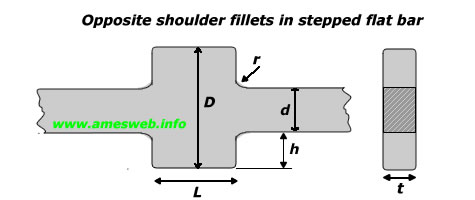
|
|
Tension |
|
|
$$0.1\le \frac { h }{ r } \le 2.0$$ |
$$2\le \frac { h }{ r } \le 20$$ |
|
$${ C }_{ 1 }=1.006+1.008\sqrt { h/r } -0.044h/r$$ |
$${ C }_{ 1 }=1.020+1.009\sqrt { h/r } -0.048h/r$$ |
|
$${ C }_{ 2 }=-0.115-0.584\sqrt { h/r } +0.315h/r$$ |
$${ C }_{ 2 }=-0.065-0.165\sqrt { h/r } -0.007h/r$$ |
|
$${ C }_{ 3 }=0.245-1.006\sqrt { h/r } -0.257h/r$$ |
$${ C }_{ 3 }=-3.459+1.266\sqrt { h/r } -0.016h/r$$ |
|
$${ C }_{ 4 }=-0.135+0.582\sqrt { h/r } -0.017h/r$$ |
$${ C }_{ 4 }=3.505-2.109\sqrt { h/r } +0.069h/r$$ |
$${ K }_{ t }={ C }_{ 1 }+{ C }_{ 2 }\frac { 2h }{ D } +{ C }_{ 3 }{ (\frac { 2h
}{ D } ) }^{ 2 }+{ C }_{ 4 }{ (\frac { 2h }{ D } ) }^{ 3 }$$
where
$$\frac { L }{ D } >-1.89(\frac { r }{ d } -0.15)+5.5$$ |
|
$${ \sigma }_{ nom }=P/td$$ |
|
$${ \sigma }_{ max }={ K }_{ t }{ \sigma }_{ nom }$$ |
|
Bending |
 |
|
$$0.1\le \frac { h }{ r } \le 2.0$$ |
$$2\le \frac { h }{ r } \le 20$$ |
|
$${ C }_{ 1 }=1.006+0.967\sqrt { h/r } +0.013h/r$$ |
$${ C }_{ 1 }=1.058+1.002\sqrt { h/r } -0.038h/r$$ |
|
$${ C }_{ 2 }=-0.270-2.372\sqrt { h/r } +0.708h/r$$ |
$${ C }_{ 2 }=-3.652+1.639\sqrt { h/r } -0.436h/r$$ |
|
$${ C }_{ 3 }=0.662+1.157\sqrt { h/r } -0.908h/r$$ |
$${ C }_{ 3 }=6.170-5.687\sqrt { h/r } +1.175h/r$$ |
|
$${ C }_{ 4 }=-0.405+0.249\sqrt { h/r } -0.200h/r$$ |
$${ C }_{ 4 }=-2.558+3.046\sqrt { h/r } -0.701h/r$$ |
$${ K }_{ t }={ C }_{ 1 }+{ C }_{ 2 }\frac { 2h }{ D } +{ C }_{ 3 }{ (\frac { 2h
}{ D } ) }^{ 2 }+{ C }_{ 4 }{ (\frac { 2h }{ D } ) }^{ 3 }$$
where
$$\frac { L }{ D } >-2.05(\frac { r }{ d } -0.025)+2$$ |
|
$${ \sigma }_{ nom }={ 6M }/{ t{ d }^{ 2 } }$$ |
|
$${ \sigma }_{ max }={ K }_{ t }{ \sigma }_{ nom }$$ |
|
|
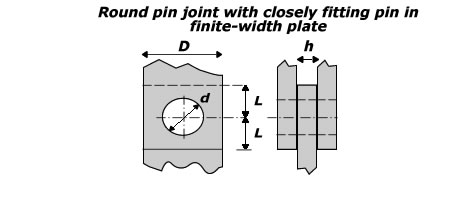
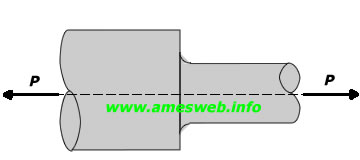
Tension |

|
|
For $$0.15\le \frac { d }{ D } \le 0.75,\quad \frac { L }{ D } \ge 1$$ |
|
$${ K }_{ ta }=12.882-52.714\frac { d }{ D } +89.762{ (\frac { d }{ D } ) }^{ 2
}-51.667{ (\frac { d }{ D } ) }^{ 3 }$$ |
|
$${ K }_{ tb }=0.2880+8.820\frac { d }{ D } -23.196{ (\frac { d }{ D } ) }^{ 2
}+29.167{ (\frac { d }{ D } ) }^{ 3 }$$ |
Nominal stress based on net section:
$${ \sigma }_{ na }=P/(D-d)h$$ |
Nominal stress based on bearing area:
$${ \sigma }_{ nb }=P/dh$$ |
|
$${ \sigma }_{ max\_ a }={ K }_{ t }{ \sigma }_{ na }$$ |
|
$${ \sigma }_{ max\_ b }={ K }_{ t }{ \sigma }_{ nb }$$ |
|
|
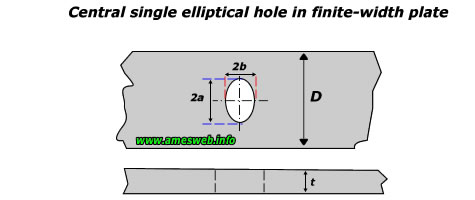
Tension |
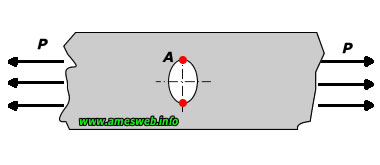
|
|
For 0.5 ≤ a/b ≤ 10.0 |
|
$${ C }_{ 1 }=1.000-0.000\sqrt { a/b } +2.000a/b$$ |
|
$${ C }_{ 2 }=-0.351-0.021\sqrt { a/b } -2.483a/b$$ |
|
$${ C }_{ 3 }=3.621-5.183\sqrt { a/b } +4.494a/b$$ |
|
$${ C }_{ 4 }=-2.270+5.204\sqrt { a/b } -4.011a/b$$ |
|
$${ K }_{ tA }={ C }_{ 1 }+{ C }_{ 2 }\frac { 2a }{ D } +{ C }_{ 3 }{ (\frac {
2a }{ D } ) }^{ 2 }+{ C }_{ 4 }{ (\frac { 2a }{ D } ) }^{ 3 }$$ |
|
$${ \sigma }_{ nom }=P/[(D-2a)t]$$ |
|
$${ \sigma }_{ A }={ K }_{ tA }{ \sigma }_{ nom }$$ |
|
In-Plane Bending |
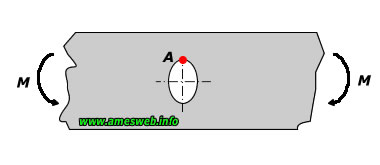
|
|
0.4 ≤ 2a/D ≤ 1.0, 1.0 ≤ a/b ≤ 2.0 |
|
$${ C }_{ 1 }=3.465-3.739\sqrt { a/b } +2.274a/b$$ |
|
$${ C }_{ 2 }=-3.841+5.582\sqrt { a/b } -1.741a/b$$ |
|
$${ C }_{ 3 }=2.376-1.843\sqrt { a/b } -0.534a/b$$ |
|
$${ K }_{ tA }={ C }_{ 1 }+{ C }_{ 2 }\frac { 2a }{ D } +{ C }_{ 3 }{ (\frac {
2a }{ D } ) }^{ 2 }$$ |
|
$${ \sigma }_{ nom }=12Ma/([{ D }^{ 3 }-8{ a }^{ 3 }]t)$$ |
|
$${ \sigma }_{ max }={ \sigma }_{ A }={ K }_{ tA }{ \sigma }_{ nom }$$ |
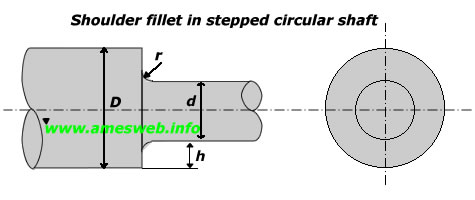
|
|
Tension |
|
|
$$0.1\le h/r\le 2.0$$ |
$$2.0\le h/r\le 20.0$$ |
|
$${ C }_{ 1 }=0.926+1.157\sqrt { h/r } -0.099h/r$$ |
$${ C }_{ 1 }=1.200+0.860\sqrt { h/r } -0.022h/r$$ |
|
$${ C }_{ 2 }=0.012-3.036\sqrt { h/r } +0.961h/r$$ |
$${ C }_{ 2 }=-1.805-0.346\sqrt { h/r } -0.038h/r$$ |
|
$${ C }_{ 3 }=-0.302+3.977\sqrt { h/r } -1.744h/r$$ |
$${ C }_{ 3 }=2.198-0.486\sqrt { h/r } +0.165h/r$$ |
|
$${ C }_{ 4 }=0.365-2.098\sqrt { h/r } +0.878h/r$$ |
$${ C }_{ 4 }=-0.593-0.028\sqrt { h/r } -0.106h/r$$ |
|
$${ K }_{ t }={ C }_{ 1 }+{ C }_{ 2 }(2h/D)+{ { C }_{ 3 }(2h/D) }^{ 2 }+{ { C
}_{ 4 }(2h/D) }^{ 3 }$$ |
|
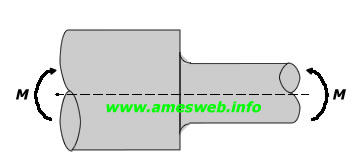
$${ \sigma }_{ nom }={ 4P }/{ \pi { d }^{ 2 } }$$ |
|
$${ \sigma }_{ max }={ K }_{ t }{ \sigma }_{ nom }$$ |
|
Bending |
|
|
$$0.1\le h/r\le 2.0$$ |
$$2.0\le h/r\le 20.0$$ |
|
$${ C }_{ 1 }=0.947+1.206\sqrt { h/r } -0.131h/r$$ |
$${ C }_{ 1 }=1.232+0.832\sqrt { h/r } -0.008h/r$$ |
|
$${ C }_{ 2 }=0.022-3.405\sqrt { h/r } +0.915h/r$$ |
$${ C }_{ 2 }=-3.813+0.968\sqrt { h/r } -0.260h/r$$ |
|
$${ C }_{ 3 }=0.869+1.777\sqrt { h/r } -0.555h/r$$ |
$${ C }_{ 3 }=7.423-4.868\sqrt { h/r } +0.869h/r$$ |
|
$${ C }_{ 4 }=-0.810+0.422\sqrt { h/r } -0.260h/r$$ |
$${ C }_{ 4 }=-3.839+3.070\sqrt { h/r } -0.600h/r$$ |
|
$${ K }_{ t }={ C }_{ 1 }+{ C }_{ 2 }(2h/D)+{ { C }_{ 3 }(2h/D) }^{ 2 }+{ { C
}_{ 4 }(2h/D) }^{ 3 }$$ |
|
$${ \sigma }_{ nom }={ 32M }/{ \pi { d }^{ 3 } }$$ |
|
$${ \sigma }_{ max }={ K }_{ t }{ \sigma }_{ nom }$$ |
|
Torsion |
|
|
$$0.25\le h/r\le 4.0$$ |
|
$${ C }_{ 1 }=0.905+0.783\sqrt { h/r } -0.075h/r$$ |
|
$${ C }_{ 2 }=-0.437-1.969\sqrt { h/r } +0.553h/r$$ |
|
$${ C }_{ 3 }=1.557+1.073\sqrt { h/r } -0.578h/r$$ |
|
$${ C }_{ 4 }=-1.061+0.171\sqrt { h/r } +0.086h/r$$ |
|
$${ K }_{ t }={ C }_{ 1 }+{ C }_{ 2 }(2h/D)+{ { C }_{ 3 }(2h/D) }^{ 2 }+{ { C
}_{ 4 }(2h/D) }^{ 3 }$$ |
|
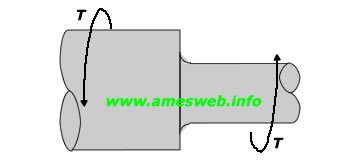
$${ \tau }_{ nom }={ 16T }/{ \pi { d }^{ 3 } }$$ |
|
$${ \tau }_{ max }={ K }_{ t }{ \tau }_{ nom }$$ |
|
|
Tension |
|
|
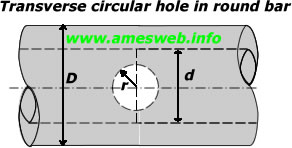
$$d/D\le 0.9\quad ,\quad 2r/D\le 0.45$$ |
|
$${ C }_{ 1 }=3.0$$ |
|
$${ C }_{ 2 }=0.427-6.770\frac { d }{ D } +22.698{ (\frac { d }{ D } ) }^{ 2
}-16.670{ (\frac { d }{ D } ) }^{ 3 }$$ |
|
$${ C }_{ 3 }=11.357+15.665\frac { d }{ D } -60.929{ (\frac { d }{ D } ) }^{ 2
}+41.501{ (\frac { d }{ D } ) }^{ 3 }$$ |
|
$${ K }_{ t }={ C }_{ 1 }+{ C }_{ 2 }\frac { 2r }{ D } +{ C }_{ 3 }{ \left(
\frac { 2r }{ D } \right) }^{ 2 }$$ |
|
$${ \sigma }_{ nom }=\frac { 4P }{ \pi ({ D }^{ 2 }-{ d }^{ 2 }) } $$ |
|
$${ \sigma }_{ max }={ \sigma }_{ A }={ K }_{ t }{ \sigma }_{ nom }$$ |
|
Bending |
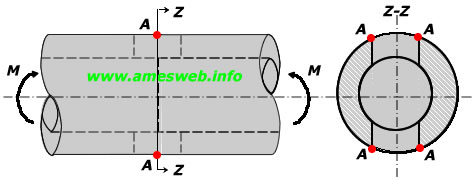
|
|
$$d/D\le 0.9\quad ,\quad 2r/D\le 0.4$$ |
|
$${ C }_{ 1 }=3.0$$ |
|
$${ C }_{ 2 }=-6.250-0.585\frac { d }{ D } +3.115{ (\frac { d }{ D } ) }^{ 2 }$$ |
|
$${ C }_{ 3 }=41.000-1.071\frac { d }{ D } -6.746{ (\frac { d }{ D } ) }^{ 2 }$$ |
|
$${ C }_{ 4 }=-45.000+1.389\frac { d }{ D } +13.889{ (\frac { d }{ D } ) }^{ 2
}$$ |
|
$${ K }_{ t }={ C }_{ 1 }+{ C }_{ 2 }\frac { 2r }{ D } +{ C }_{ 3 }{ \left(
\frac { 2r }{ D } \right) }^{ 2 }+{ C }_{ 4 }{ \left( \frac { 2r }{ D } \right)
}^{ 3 }$$ |
|
$${ \sigma }_{ nom }=\frac { 32MD }{ \pi ({ D }^{ 4 }-{ d }^{ 4 }) } $$ |
|
$${ \sigma }_{ max }={ \sigma }_{ A }={ K }_{ t }{ \sigma }_{ nom }$$ |
|
Torsion |
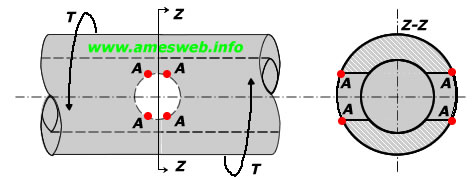
|
|
$$d/D\le 0.8\quad ,\quad 2r/D\le 0.4$$ |
|
$${ C }_{ 1 }=4.0$$ |
|
$${ C }_{ 2 }=-6.055+3.184\frac { d }{ D } -3.461{ (\frac { d }{ D } ) }^{ 2 }$$ |
|
$${ C }_{ 3 }=32.764-30.121\frac { d }{ D } +39.887{ (\frac { d }{ D } ) }^{ 2
}$$ |
|
$${ C }_{ 4 }=-38.330+51.542\sqrt { d/D } -27.483\frac { d }{ D } $$ |
|
$${ K }_{ t }={ C }_{ 1 }+{ C }_{ 2 }\frac { 2r }{ D } +{ C }_{ 3 }{ \left(
\frac { 2r }{ D } \right) }^{ 2 }+{ C }_{ 4 }{ \left( \frac { 2r }{ D } \right)
}^{ 3 }$$ |
|
$${ \sigma }_{ max }={ \sigma }_{ A }={ K }_{ t }{ \tau }_{ nom }$$ |
|
$${ \tau }_{ nom }=\frac { 16TD }{ \pi ({ D }^{ 4 }-{ d }^{ 4 }) } $$ |
|
$${ \tau }_{ max }={ \tau }_{ A }={ 0.5K }_{ t }{ \tau }_{ nom }$$ |
|
|
Tension |
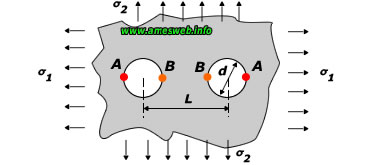
|
|
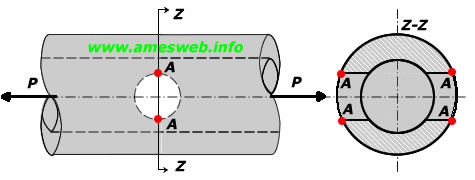
for 0 ≤ d/L<1 |
|
$${ \sigma }_{ max }={ K }_{ t }\sigma $$ |
Uniaxial tension parallel to row of holes (σ1 = σ , σ2 = 0)
$${ K }_{ t }=3.000-0.712d/L+0.271{ (d/L) }^{ 2 }$$ |
Uniaxial tension normal to row of holes (σ2 = σ , σ1 = 0)
$${ \sigma }_{ max }={ \sigma }_{ B }={ K }_{ t }{ \sigma }_{ nom }\quad ,\quad
{ \sigma }_{ nom }\quad =\frac { \sigma \sqrt { 1-{ \left( d/L \right) }^{ 2 } }
}{ 1-d/L } $$
$${ K }_{ t }=3.000-3.0018d/L+1.0099{ (d/L) }^{ 2 }$$ |
Biaxial tension (σ2 = σ, σ1 = σ)
$${ \sigma }_{ max }={ \sigma }_{ B }={ K }_{ t }{ \sigma }_{ nom }\quad ,\quad
{ \sigma }_{ nom }\quad =\frac { \sigma \sqrt { 1-{ \left( d/L \right) }^{ 2 } }
}{ 1-d/L } $$
$${ K }_{ t }=2.000-2.119d/L+2.493{ (d/L) }^{ 2 }-1.372{ (d/L) }^{
3 }$$
|