SINGLE ELLIPTICAL HOLE IN A FINITE-WIDTH PLATE

Single elliptical hole in a finite width plate. Theoretical stress concentration factors (Kt)calculator for tension and in-plane bending loads.

Single elliptical hole in finite-width plate
 INPUT PARAMETERS
Parameter Value
Plate width [D]
Semi-major axis [2a]
Semi-minor axis [2b]
Plate thickness [t]
Tension force [P]
In-plane bending moment [M]

Note: Use dot "." as decimal separator.

 


 RESULTS
LOADING TYPE - TENSION
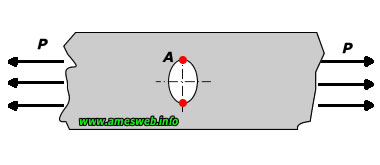
Stress concentration factor for single elliptical hole in finite-width plate under tension
Parameter Value
Stress concentration factor at point A [Kt] * --- ---
Nominal tension stress [σnom ] o ---
Maximum tension stress at Point - A [σmax ] ---
LOADING TYPE - IN-PLANE BENDING
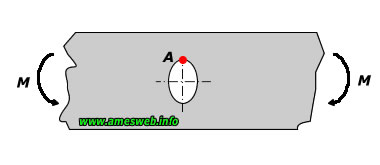
Stress concentration factor for single elliptical hole in finite-width plate under in-plane bending
Parameter Value
Stress concentration factor at point - A [KtA] * --- ---
Nominal tension stress [σnom ] + ---
Maximum tension stress at Point - A [σmax ] ---

Note 1: * Geometry rises σnom by a factor of Kt . (Kt = σmax/σnom)

Note 2: o σnom= P/[(1-2a/D)Dt] (Nominal tension stress at the plate cross section due to tension load)

Note 3: + σnom  = 12Ma/[t(D3-8a3)] (Nominal tension stress)

Note 4: KtA  = (σnom/σmax) Theoretical stress concentration factor at point A in elastic range


Definitions:

Stress Concentration Factor: Dimensional changes and discontinuities of a member in a loaded structure causes variations of stress and high stresses concentrate near these dimensional changes. This situation of high stresses near dimensional changes and discontinuities of a member (holes, sharp corners, cracks etc.) is called stress concentration. The ratio of peak stress near stress riser to average stress over the member is called stress concentration factor.

Kt: Theoretical stress concentration factor in elastic range = (σmax/σnom)

Formulas:

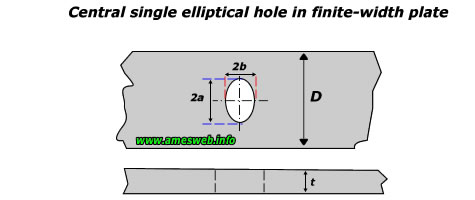
Single elliptical hole in finite-width plate
Tension
Stress concentration factor for single elliptical hole in finite-width plate under tension
For 0.5 ≤ a/b ≤ 10.0
$${ C }_{ 1 }=1.000-0.000\sqrt { a/b } +2.000a/b$$
$${ C }_{ 2 }=-0.351-0.021\sqrt { a/b } -2.483a/b$$
$${ C }_{ 3 }=3.621-5.183\sqrt { a/b } +4.494a/b$$
$${ C }_{ 4 }=-2.270+5.204\sqrt { a/b } -4.011a/b$$
$${ K }_{ tA }={ C }_{ 1 }+{ C }_{ 2 }\frac { 2a }{ D } +{ C }_{ 3 }{ (\frac { 2a }{ D } ) }^{ 2 }+{ C }_{ 4 }{ (\frac { 2a }{ D } ) }^{ 3 }$$
$${ \sigma }_{ nom }=P/[(D-2a)t]$$
$${ \sigma }_{ A }={ K }_{ tA }{ \sigma }_{ nom }$$
In-Plane Bending
Stress concentration factor for single elliptical hole in finite-width plate under in-plane bending
 0.4 ≤ 2a/D ≤ 1.0,  1.0 ≤ a/b ≤ 2.0
$${ C }_{ 1 }=3.465-3.739\sqrt { a/b } +2.274a/b$$
$${ C }_{ 2 }=-3.841+5.582\sqrt { a/b } -1.741a/b$$
$${ C }_{ 3 }=2.376-1.843\sqrt { a/b } -0.534a/b$$
$${ K }_{ tA }={ C }_{ 1 }+{ C }_{ 2 }\frac { 2a }{ D } +{ C }_{ 3 }{ (\frac { 2a }{ D } ) }^{ 2 }$$
$${ \sigma }_{ nom }=12Ma/([{ D }^{ 3 }-8{ a }^{ 3 }]t)$$
$${ \sigma }_{ max }={ \sigma }_{ A }={ K }_{ tA }{ \sigma }_{ nom }$$

Reference: