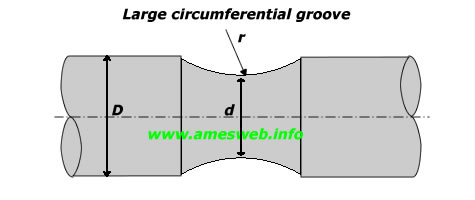
LARGE CIRCUMFERENTIAL GROOVE ON A CIRCULAR SHAFT

Large circumferential groove on a circular shaft. Stress concentration factors (K_t) calculator for tension, bending and torsion loads.

INPUT PARAMETERS
Parameter	Value
Diameter of larger shaft section [D]		mm cm m inch ft
Diameter of smaller shaft section [d]
Radius [r]
Tension force [P]		N kN lbf
Bending moment [M]		N*m lbf*in lbf*ft
Torque [T]

Note:Use dot "." as decimal separator.

Please Wait... 

RESULTS
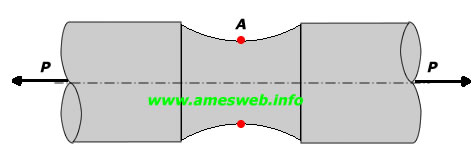
LOADING TYPE - TENSION
Parameter	Value
Stress concentration factor[Kt] *	---	---
Nominal tension stress at shaft [σnom ] o	---	MPa psi ksi
Maximum tension stress due to tension load (at Point-A) [σmax ]	---
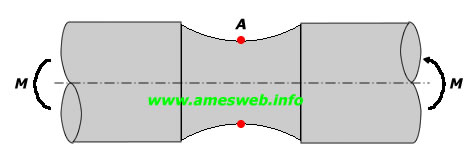
LOADING TYPE - BENDING
Parameter	Value
Stress concentration factor [Kt] *	---	---
Nominal tension stress at shaft [σnom ] +	---	MPa psi ksi
Maximum tension stress due to bending (at Point-A) [σmax ]	---
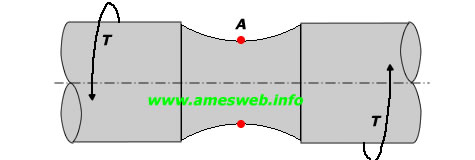
LOADING TYPE - TORSION
Parameter	Value
Stress concentration factor [Kt] **	---	---
Nominal shear stress at shaft [τnom ] x	---	MPa psi ksi
Maximum shear stress due to torsion (at Point-A) [τmax ]	---

Note 1: Maximum stress is occured at point A

Note 2: * Geometry rises σ_nom by a factor of K_t.  ( K_t = σ_max/σ_nom)

Note 3: ** Geometry rises τ_nom by a factor of K_t.  ( K_t = τ_max/τ_nom)

Note 4: ^o σ_nom= 4P/(πd²) (Nominal tension stress occurred due to tension load)

Note 5: ⁺ σ_nom = 32M/(πd³) (Nominal tension stress occured due to bending)

Note 6: ^x τ_nom = 16T/(πd³) (Nominal shear stress occureed due to  torsion)

Definitions:

Stress Concentration Factor: Dimensional changes and discontinuities of a member in a loaded structure causes variations of stress and high stresses concentrate near these dimensional changes. This situation of high stresses near dimensional changes and discontinuities of a member (holes, sharp corners, cracks etc.) is called stress concentration. The ratio of peak stress near stress riser to average stress over the member is called stress concentration factor.

K_t: Theoretical stress concentration factor in elastic range = (σ_max/σ_nom)

Formulas:

Tension

$$0.3\quad \le \quad \frac { r }{ d } \le \quad 1.0$$ , $$1.005\quad \le \quad \frac { D }{ d } \le \quad 1.10$$

$${ C }_{ 1 }=-81.39+153.10(D/d)-70.49{ (D/d) }^{ 2 }$$

$${ C }_{ 2 }=119.64-221.81(D/d)+101.93{ (D/d) }^{ 2 }$$

$${ C }_{ 3 }=-57.88+107.33(D/d)-49.34{ (D/d) }^{ 2 }$$

$${ K }_{ t }={ C }_{ 1 }+{ C }_{ 2 }\frac { r }{ d } +{ C }_{ 3 }{ (\frac { r }{ d } ) }^{ 2 }$$

$${ \sigma }_{ nom }=4P/\pi { d }^{ 2 }$$

$${ \sigma }_{ max }={ \sigma }_{ A }={ K }_{ t }{ \sigma }_{ nom }$$

Bending

$$0.3\quad \le \quad \frac { r }{ d } \le \quad 1.0$$ , $$1.005\quad \le \quad \frac { D }{ d } \le \quad 1.10$$

$${ C }_{ 1 }=-39.58+73.22(D/d)-32.46{ (D/d) }^{ 2 }$$

$${ C }_{ 2 }=-9.477+29.41(D/d)-20.13{ (D/d) }^{ 2 }$$

$${ C }_{ 3 }=82.46-166.96(D/d)+84.58{ (D/d) }^{ 2 }$$

$${ K }_{ t }={ C }_{ 1 }+{ C }_{ 2 }\frac { r }{ d } +{ C }_{ 3 }{ (\frac { r }{ d } ) }^{ 2 }$$

$${ \sigma }_{ nom }=32M/\pi { d }^{ 3 }$$

$${ \sigma }_{ max }={ \sigma }_{ A }={ K }_{ t }{ \sigma }_{ nom }$$

Torsion

$$0.3\quad \le \quad \frac { r }{ d } \le \quad 1.0$$ , $$1.005\quad \le \quad \frac { D }{ d } \le \quad 1.10$$

$${ C }_{ 1 }=-35.16+67.57(D/d)-31.28{ (D/d) }^{ 2 }$$

$${ C }_{ 2 }=79.13-148.37(D/d)+69.09{ (D/d) }^{ 2 }$$

$${ C }_{ 3 }=-50.34+94.67(D/d)-44.26{ (D/d) }^{ 2 }$$

$${ K }_{ t }={ C }_{ 1 }+{ C }_{ 2 }\frac { r }{ d } +{ C }_{ 3 }{ (\frac { r }{ d } ) }^{ 2 }$$

$${ \tau }_{ nom }=16T/\pi { d }^{ 3 }$$

$${ \tau }_{ max }=\tau _{ A }={ K }_{ t }{ \tau }_{ nom }$$

Reference:

• Pilkey, W. D..(2005). Formulas for Stress, Strain, and Structural Matrices Formulas for Stress, Strain, and Structural Matrices .2nd Edition John Wiley & Sons