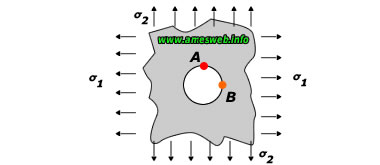
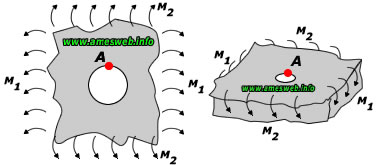
SINGLE CIRCULAR HOLE IN AN INFINITE PLATE

single circular hole in an infinite plate. Stress concentration factors (K_t) for tension and transverse (out-of-plane) bending loads.

INPUT PARAMETERS
Parameter	Value
Hole diameter [d]		mm cm m inch ft
Plate thickness [t]
In-plane normal stress-1 [σ1]		MPa psi ksi
Transverse (out-of-plane) bending moment [M1]		N*m lbf*in lbf*ft

Note: Use dot "." as decimal separator.

Please Wait... 

RESULTS
LOADING TYPE - IN-PLANE NORMAL STRESS
Parameter	Value
UNIAXIAL STRESS ( σ2=0)
Stress concentration factor for point-A [KtA]*	3	---
Stress concentration factor for point-B [KtB]*	-1
Maximum tension stress at point-A [σA]	---	MPa psi ksi
Maximum tension stress at point-B [σB]	---
BIAXIAL STRESS ( σ2=σ1)
Stress concentration factor for point-A [KtA]*	2	---
Stress concentration factor for point-B [KtB]*	2
Maximum tension stress at point-A [σA]	---	MPa psi ksi
Maximum tension stress at point-B [σB]	---
BIAXIAL STRESS ( σ2 = -σ1) (PURE SHEAR)
Stress concentration factor for point-A [KtA]*	4	---
Stress concentration factor for point-B [KtB]*	4
Maximum tension stress at point-A [σA]	---	MPa psi ksi
Maximum tension stress at point-B [σB]	---
LOADING TYPE - TRANSVERSE (OUT-OF-PLANE) BENDING
SIMPLE BENDING(M1 = M , M2 = 0)
Stress concentration factor at point A [KtA] *	---	---
Nominal tension stress [σnom] #	---	MPa psi ksi
Maximum tension stress (at Point-A) [σmax]	---
ISOTROPIC BENDING (M1 = M , M2 = M)
Stress concentration factor at point A [KtA] *	2	---
Nominal tension stress [σnom] #	---	MPa psi ksi
Maximum tension stress (at Point-A) σmax[]	---

Note 1: * Geometry rises σ_nom by a factor of K_t . (K_t = σ_max/σ_nom)

Note 2: ^# σ_nom = 6M₁/t² (Nominal tension stress at the edge of the hole due to bending)

Note 3: K_tA  = (σ_max/σ_nom) Theoretical stress concentration factor at point A in elastic range

Note 4: K_tB  = (σ_max/σ_nom) Theoretical stress concentration factor at point B in elastic range

Definitions:

Stress Concentration Factor: Dimensional changes and discontinuities of a member in a loaded structure causes variations of stress and high stresses concentrate near these dimensional changes. This situation of high stresses near dimensional changes and discontinuities of a member (holes, sharp corners, cracks etc.) is called stress concentration. The ratio of peak stress near stress riser to average stress over the member is called stress concentration factor.

K_t: Theoretical stress concentration factor in elastic range = (σ_max/σ_nom)

Formulas:

Tension

Uniaxial tension (σ2=0) σmax = Ktσ1 σA = 3σ1 (Kt=3) σB = -σ1 (Kt=-1)

Biaxial Tension For σ2 = σ1 , σA = σB = 2σ1 (Kt=2) For σ2 = -σ1(pure shear stress), σA = -σB = 4σ1 (Kt=4)

Transverse Bending

σmax = Ktσ, σ = 6M/t 2

Simple bending (M1=M, M 2=0) For 0 ≤ d/t ≤ 7.0 , σmax = σA $${ K }_{ t }=3.000-0.947\sqrt { d/t } +0.192d/t$$

Isotropic bending (M1 = M 2 = M) σmax = σA Kt=2 (independent of d/t)

Reference:

• Pilkey, W. D..(2005). Formulas for Stress, Strain, and Structural Matrices Formulas for Stress, Strain, and Structural Matrices .2nd Edition John Wiley & Sons