V-shaped circumferential groove on a shaft. Stress concentration factors (Kt) calculator for torsion loads.
Note: Use dot "." as decimal separator.
|
RESULTS |
|
LOADING TYPE - TORSION |
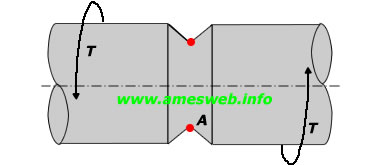
|
|
Parameter |
Value |
|
Stress concentration factorn [Kt]
* |
---
|
--- |
|
Nominal shear stress at shaft [τnom ] x |
---
|
|
|
Maximum shear stress due to torsion (at Point-A) [τmax ] |
---
|
Note 1: Maximum stress is occured at point A.
Note 2: * Geometry rises τnom by a factor of Kt. (Kt = τnom/τmax)
Note 3: x τnom= 16T/(πd3) (Nominal shear stress occurred due to torsion)
Note 4: V-shaped stress concentration factor is dependent on U-shaped stress
concentration factor. Input parameters shall satisfy both cases.